6.6

Consider the representation of the ternary relationship of Figure 6.29a using the binary relationships illustrated in Figure 6.29b (attributes not shown).

a. Show a simple instance of $E$,$A$,$B$,$C$,$R_A$,$R_B$, and $R_C$ that cannot correspond to any instance of $A$, $B$, $C$, and $R$.

b. Modify the E-R diagram of Figure 6.29b to introduce constraints that will guarantee that any instance of $E$,$A$,$B$,$C$,$R_A$,$R_B$, and $R_C$ that satisfies the constraints will correspond to an instance of $A$, $B$, $C$, and $R$.

c. Modify the preceding translation to handle total participation constraints on the ternary relationship.

---

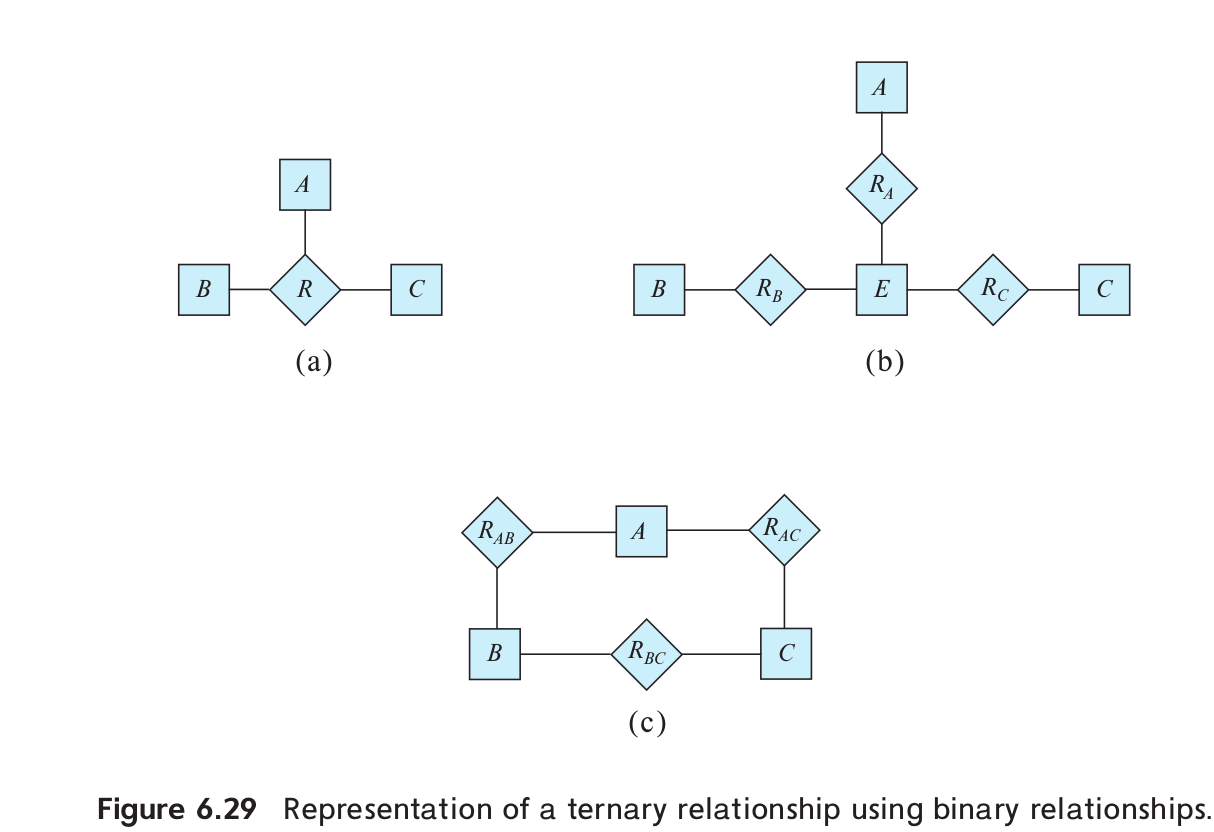
a. Let $E=\{e_1,e_2\}$, $A=\{a_1,a_2\}$, $B=\{b_1\}$, $C=\{c_1\}$, $R_A=\{(e_1,a_1),(e_2,a_2)\}$, $R_B=\{(e_1,b_1)\}$, $R_C=\{(e_1,c_1)\}$. We see that because of the tuple $(e_2,a_2)$, no instance of $A$,$B$,$C$, and $R$ exists that correspond to $E$,$R_A$,$R_B$, and $R_C$

b. See Figure 6.105. The idea is to introduce total participation constraints between $E$ and the relationships $R_A$, $R_B$, $R_C$ so that every tuple in $E$ has a relationship with $A$,$B$, and $C$.

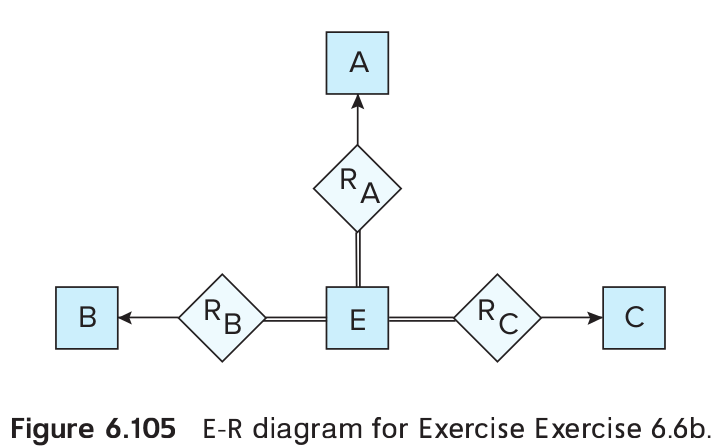
c. Suppose $A$ totally participates in the relationship $R$, then introduce a total participation constraint between $A$ and $R_A$, and similarly for $B$ and $C$.