AGT MID 21-22 solution

Q3 (a) For a planar graph G with n number of vertices and e number of edges with r regions, prove by method of induction that n-e+r = 2

Theorem (Euler’s Formula): For a connected planar graph G, with n vertices, e edges, and r regions (faces, including the outer face):

$n-e+r=2$

Proof (by Induction on the number of edges, e):

1. Base Case: $e=0$,Since G is given a connected.

• If $e=0$, and the graph is connected, then $n=1$ (single vertex).
• There’s only one region (the outer region), so $r=1$.
• $n-e+r=1-0+1=2$. The formula holds.

2. Inductive Hypothesis:

   Assume the formula holds for all connected planar graphs with $k$ edges, where $k\ge 0$:

   $n-k+r=2$

3. Inductive Step:

   Consider a connected planar graph G’ with $k+1$ edges. We want to show that $n^{\prime }-(k+1)+r^{\prime }=2$, where $n^{\prime }$ and $r^{\prime }$ are the number of vertices and regions in G’, respectively.

   • Case 1: G’ has a cycle.

     • Remove one edge from any cycle in G’. Call this removed edge ‘x’.
     • This creates a new graph G, with:
       • $n=n^{\prime }$ (same vertices)
       • $e=(k+1)-1=k$ (one less edge)
       • $r=r^{\prime }-1$ (removing an edge from a cycle merges two regions)
     • By the inductive hypothesis, for G: $n-k+(r^{\prime }-1)=2$
     • Rearrange: $n^{\prime }-k-1+r^{\prime }=2$
     • Substitute $k+1=e^{\prime }$: $n^{\prime }-e^{\prime }+r^{\prime }=2$

   • If G is a tree, then $k=n-1$ and $r=1$, so

     • $n-m+r==n-(n-1)+1==n-n+1+1==2$ satisfy

   • $n^{\prime }-e^{\prime }+r^{\prime }=2$.

4. conclusion By method of induction equation is true.

3 (b) llustrate with suitable example (considering a labelled tree T with (343) at least 9 vertices) and converting T into its equivalent Prufer Sequence S and vice versa.

Link

4 (b) Illustrate the situation when Dijkstra’s Algorithm may fail to find the shortest path but Bellman-Ford Algorithm may succeed. And also mention the situation when Bellman-Ford Algorithm may fail (illustrate with an example).

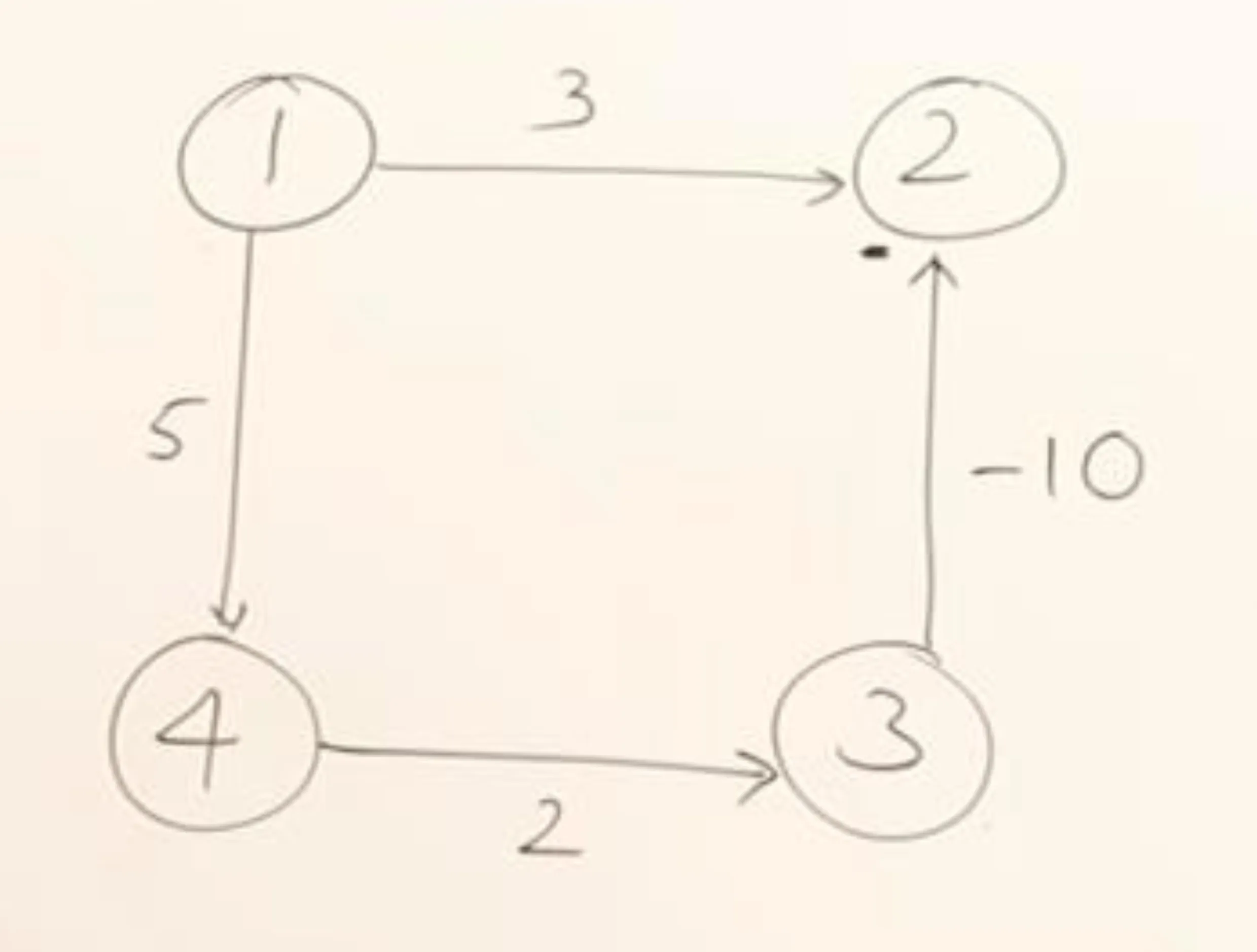
1. Dijkstra’s Algorithm Failure (Negative Edge Weights):

• Scenario: Dijkstra’s algorithm fails when the graph contains negative edge weights. It’s designed for graphs with non-negative edge weights only.

• Why it Fails: Dijkstra’s algorithm greedily selects the closest unvisited vertex. It assumes that once a vertex is “visited” (its shortest distance is finalized), there’s no possibility of finding a shorter path to it later. Negative edges violate this assumption. link

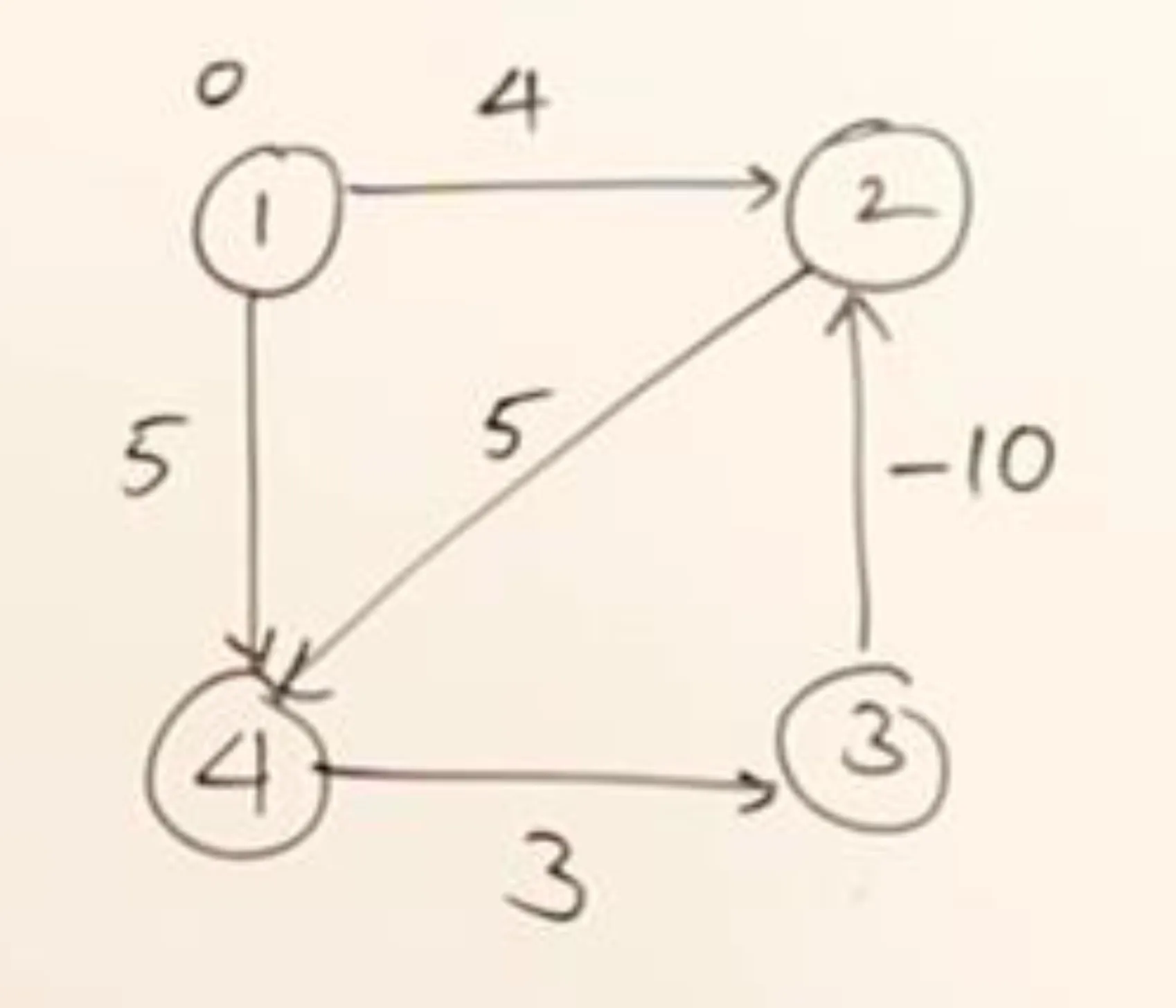
2. Bellman-Ford Algorithm Success (with Negative Edge Weights):

• Scenario: Bellman-Ford can handle graphs with negative edge weights, provided there are no negative-weight cycles reachable from the source.

• Why it Works: Bellman-Ford iteratively relaxes edges. In each iteration, it checks if going through any edge can improve the currently known shortest distance to a vertex. It performs |V| - 1 iterations (where |V| is the number of vertices). This guarantees that if a shortest path exists (no negative-weight cycles), it will be found. link

5 (b) Describe Floyd-Warshall Algorithm to find the shortest paths among all vertices.

link