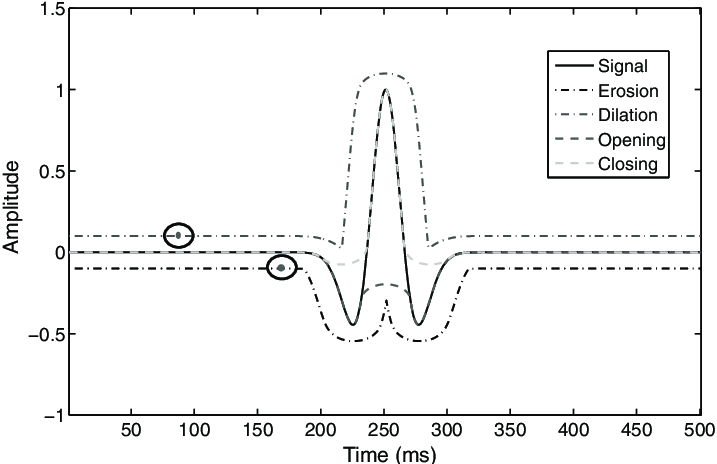
1. Introduction to Morphology

What it is: Mathematical morphology is a theory and technique for the analysis and processing of geometrical structures, based on set theory, lattice theory, topology, and random functions. It’s mostly applied to digital images but can be used on graphs, surface meshes, solids, and other spatial structures.
Core Idea: Probing an image with a small shape or template called a structuring element. The shape and size of the structuring element determine the precise effect of the operation on the image.
Basic Operators: The fundamental morphological operations are erosion, dilation, opening, and closing.
Applications:
- Noise removal
- Image segmentation
- Feature extraction
- Edge detection
- Image enhancement

2. Structuring Elements (SE)

Definition: A small binary image (matrix) used to interact with the image being processed.
Origin: The structuring element has a defined center, called the origin, which identifies the pixel being processed.
Shapes: Common shapes include squares, disks, diamonds, lines, etc. The choice of shape depends on the desired effect.
Example (3x3 square SE):
```
[1 1 1]
[1 1 1]
[1 1 1]
```
Where ‘1’ represents a pixel that is part of the SE, and ‘0’ is not.

3. Basic Operations

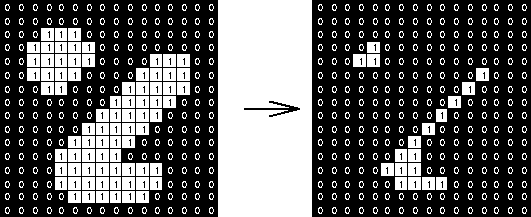
A. Erosion

Concept: Shrinks or thins objects in a binary image.
Analogy: Imagine “eroding” the boundaries of objects.
Operation: The structuring element is slid over the image. If the SE completely fits within the object (all ‘1’s of the SE align with ‘1’s in the image), the corresponding pixel in the output image is set to ‘1’. Otherwise, it’s set to ‘0’.
Mathematical Notation (for binary images): Let:
- A be the input image (a set of pixel coordinates).
- B be the structuring element.
- z be a translation vector of the origin
- $B_{z}$ be the translation of $B$ by $z$ The erosion of A by B is denoted as $A ⊖ B$ or $A ⊖ B$ and is defined as:
$A ⊖ B = {z \in E ∣ B_{z} \subseteq A}$
Effects:
- Removes small objects or details.
- Separates connected objects.
- Shrinks the size of objects.

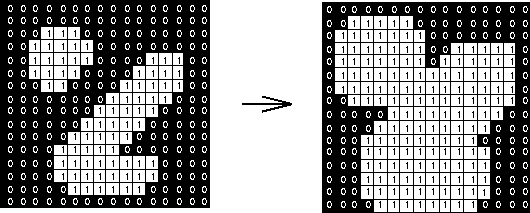
B. Dilation

Concept: Expands or thickens objects in a binary image.
Analogy: Imagine “growing” the boundaries of objects.
Operation: The SE is slid over the image. If any part of the SE overlaps with the object (at least one ‘1’ of the SE aligns with a ‘1’ in the image), the corresponding pixel in the output image is set to ‘1’. Otherwise, it’s set to ‘0’.
Mathematical Notation (for binary images): The dilation of A by B is denoted as $A \oplus B$ and is defined as:

$A \oplus B = {z \in E ∣ (\hat{B})_{z} \cap A \neq = \emptyset}$ Where
- $\hat{B}$ is the reflection of $B$
Effects:
- Fills small holes or gaps.
- Connects broken objects.
- Increases the size of objects.

C. Opening

Concept: Erosion followed by dilation, using the same structuring element.
Operation: First, erode the image with the SE, then dilate the result with the same SE.
Mathematical Notation: The opening of A by B is denoted as A ∘ B and is defined as: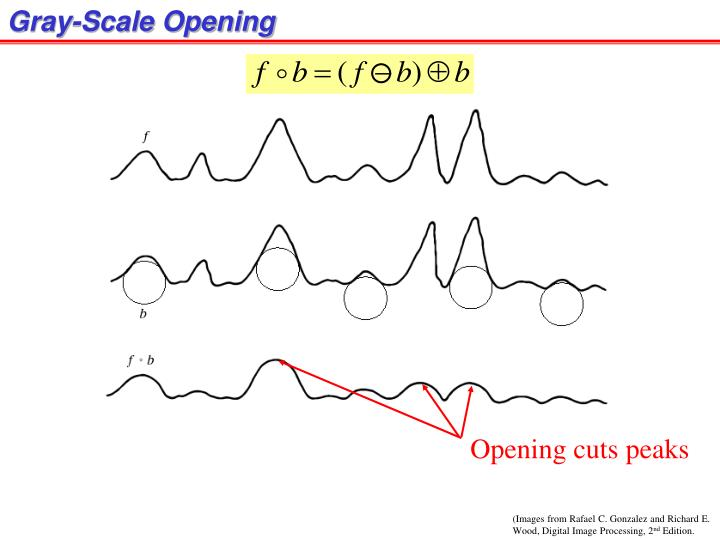

$A \circ B = (A ⊖ B) \oplus B$
Effects:
- Removes small objects and thin protrusions (smoothes from the outside).
- Preserves the general shape and size of larger objects.
- Breaks thin connections.

D. Closing

Concept: Dilation followed by erosion, using the same structuring element.
Operation: First, dilate the image with the SE, then erode the result with the same SE.
Mathematical Notation: The closing of A by B is denoted as A • B and is defined as: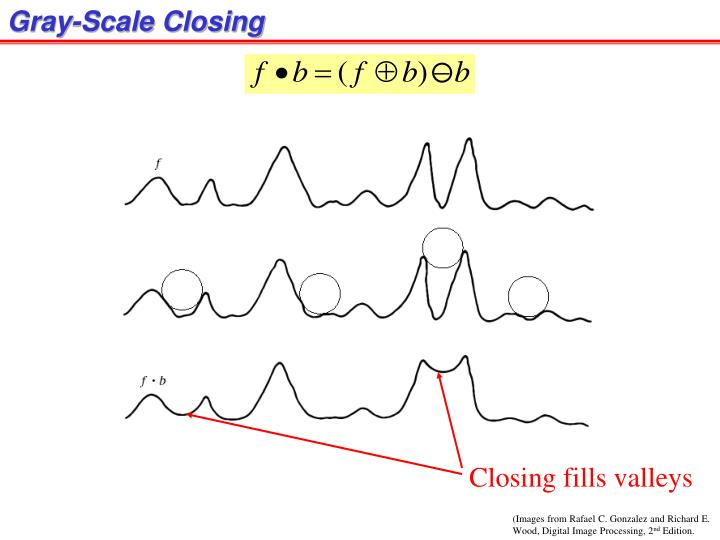

$A ∙ B = (A \oplus B) ⊖ B$
Effects:
- Fills small holes and gaps (smoothes from the inside).
- Preserves the general shape and size of objects.
- Fuses narrow breaks.

4. Top-Hat Transforms: Introduction

Purpose: Top-hat transforms are used to extract bright or dark features from an image that are smaller than the structuring element. They are particularly useful when dealing with uneven illumination or a non-uniform background.
Types:
- Bright Top-Hat (or White Top-Hat): Extracts bright features (peaks).
- Dark Top-Hat (or Black Top-Hat or Bottom-Hat): Extracts dark features (valleys).

1. Bright Top-Hat Transform

Concept: Detects bright objects or regions that “fit” within the structuring element. These objects are brighter than their surrounding pixels.
Operation:
1. Perform an opening operation on the original image using a given structuring element.
2. Subtract the opened image from the original image.
Mathematical Notation: Let:
- f be the input image (grayscale or binary).
- b be the structuring element.
- $(f \circ b)$ denote the opening of f by b.
The bright top-hat transform, $T_{w} (f)$ , is defined as:

$T_{w} (f) = f - (f \circ b)$
Explanation:
- The opening operation removes bright features smaller than the SE, smoothing the image from the outside.
- Subtracting the opened image from the original image isolates the features that were removed, leaving only those bright, small features.
Effects:
- Highlights bright objects on a darker, possibly uneven background.
- The size of the extracted features is controlled by the size of the structuring element.
Applications:
- Extracting bright text or objects from a non-uniformly lit background.
- Detecting bright spots or defects in images.

2. Dark Top-Hat (Bottom-Hat) Transform

Concept: Detects dark objects or regions that “fit” within the structuring element. These objects are darker than their surrounding pixels.
Operation:
1. Perform a closing operation on the original image using a given structuring element.
2. Subtract the original image from the closed image.
Mathematical Notation: Let:
- f be the input image (grayscale or binary).
- b be the structuring element.
- $f ∙ b$ denote the closing of f by b.
The dark top-hat transform, $T_{b} (f)$ , is defined as:

$T_{b} (f) = (f ∙ b) - f$
Explanation:
- The closing operation fills in dark features smaller than the SE, smoothing the image from the inside.
- Subtracting the original image from the closed image isolates the features that were filled in, leaving only those dark, small features.
Effects:
- Highlights dark objects on a brighter, possibly uneven background.
- The size of the extracted features is controlled by the size of the structuring element.
Applications:
- Extracting dark text or objects from a non-uniformly lit background.
- Detecting cracks, pits, or other dark defects.
- Shadow detection.

Morphological Feature Enhancement/Derivation

Expression:

$f = (f \circ 2 B) + (f \circ B - f \circ 2 B) + (f - f \circ B)$

Interpretation:

The expression combines the results of three morphological operations to produce an output image f that likely enhances features of various sizes and brightness characteristics:

$(f \circ 2 B)$ : This component represents a smoothed version of the image where features smaller than 2B have been removed. It can be considered a “base” image with larger structures preserved.
$(f \circ B - f \circ 2 B)$ : This component highlights “medium-sized” features that fall within the scale range defined by B and 2B.
$(f - f \circ B)$ : This component extracts small, bright features that are smaller than B.

Possible Application Scenario:

Consider a scenario where you are analyzing an image with objects of varying sizes and intensities:

Large, dim objects: These would be preserved in the (f o 2B) component.
Medium-sized objects: These would be highlighted in the (f o B - f o 2B) component.
Small, bright objects: These would be emphasized in the (f - f o B) component (the bright top-hat).

By summing these components, the resulting image f would simultaneously enhance large structures, medium-sized objects, and small, bright details.

Weights and Adjustments:

The expression, as written, gives equal weight to each component. In a practical application, you might introduce weighting factors to adjust the contribution of each component:

$f = w_{1} (f \circ 2 B) + w_{2} (f \circ B - f \circ 2 B) + w_{3} (f - f \circ B)$

Where $w_{1}$ , $w_{2}$ , and $w_{3}$ are weights that can be tuned to emphasize different feature types based on the specific needs of your application.

Variation 1: Additive Enhancement

Equation: $f = f + w_{1} (f \circ n B - f) + w_{2} (f - f \circ B)$
Components:
1. Scaled Dark Top-Hat: $f \circ n B - f$
  - Extracts dark features smaller than nB.
  - Weight w_1 controls enhancement strength.
2. Bright Top-Hat: $f - f \circ B$
  - Extracts bright features smaller than B.
  - Weight w_2 controls enhancement strength.
Effect: Enhances both bright and dark small-scale details in the original image f.

Variation 2: Subtractive Modification (Option 1 - Dark Feature Suppression)

Equation: $f = f - w_{1} (f \circ n B - f) - w_{2} (f \circ B - f)$
Components:
1. Scaled Dark Top-Hat: $f \circ n B - f$
  - Highlights dark features smaller than nB.
  - Weight w_1 controls subtraction strength.
2. Dark Top-Hat: $f \circ B - f$
  - Highlights dark features smaller than B.
  - Weight w_2 controls subtraction strength.
Effect: Suppresses or reduces the intensity of dark features of different scales in the original image f.

Key Parameters:

n: Scaling factor for structuring element B. Controls the size range of features affected.
B: Structuring element (shape and size). Determines the type of features influenced.
w_1, w_2: Weights. Control the strength of enhancement or suppression.

2ndSem

Explorer

Morphology Techniques