Derivation of Rotation Geometric Transformation

1. Starting with Polar Coordinates

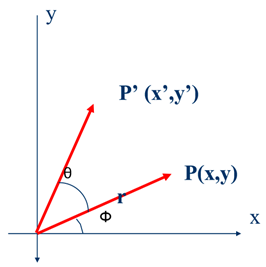
• Consider a point P with Cartesian coordinates $(x,y)$.

• We can represent the same point P using polar coordinates $(r,\alpha )$, where:

  • r is the distance from the origin to the point (the radius).
  • α (alpha) is the angle between the positive x-axis and the line connecting the origin to the point.

• The relationship between Cartesian and polar coordinates is:

  • $x=r\cos (\alpha )$
  • $y=r\sin (\alpha )$

2. Rotating the Point

• Now, let’s rotate the point P by an angle $\theta$ counterclockwise around the origin to a new position P’ with coordinates $(x^{\prime },y^{\prime })$.
• In polar coordinates, the new point P’ will have the same radius r but a new angle α + θ.
• Therefore, the Cartesian coordinates of the rotated point P’ are:
  • $x^{\prime }=r\cos (\alpha +\theta )$
  • $y^{\prime }=r\sin (\alpha +\theta )$

3. Applying Trigonometric Identities

• We can use the angle addition formulas for cosine and sine to expand the expressions for x' and y':

  • $\cos (\alpha +\theta )=\cos (\alpha )\cos (\theta )-\sin (\alpha )\sin (\theta )$
  • $\sin (\alpha +\theta )=\sin (\alpha )\cos (\theta )+\cos (\alpha )\sin (\theta )$

• Substituting these into the equations for x' and y':

  • $x^{\prime }=r[\cos (\alpha )\cos (\theta )-\sin (\alpha )\sin (\theta )]$
  • $y^{\prime }=r[\sin (\alpha )\cos (\theta )+\cos (\alpha )\sin (\theta )]$

4. Substituting Back to Cartesian Coordinates

• Recall that $x=r\cos (\alpha )$ and $y=r\sin (\alpha )$.
• Substitute these back into the equations for x' and y':
  • $x^{\prime }=(r\cos (\alpha ))\cos (\theta )-(r\sin (\alpha ))\sin (\theta )$
  • $y^{\prime }=(r\sin (\alpha ))\cos (\theta )+(r\cos (\alpha ))\sin (\theta )$
• This simplifies to:
  • $x^{\prime }=x\cos (\theta )-y\sin (\theta )$
  • $y^{\prime }=y\cos (\theta )+x\sin (\theta )$
  • $y^{\prime }=x\sin (\theta )+y\cos (\theta )$

5. Matrix Form (Homogeneous Coordinates)

• We can express these equations in matrix form using homogeneous coordinates:

  $\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}\cos (\theta )& -\sin (\theta )& 0\\ \sin (\theta )& \cos (\theta )& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$