Gaussian Pyramids

Gaussian Profile

• Definition: The Gaussian profile, also known as the Gaussian function or the normal distribution, is a bell-shaped curve defined by the following probability density function:

  $G(x,y)=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{x^2+y^2}{2{\sigma }^2}}$

  Where:

  • $G(x,y)$ represents the value of the Gaussian function at coordinates $(x,y)$.
  • $\sigma$ (sigma) is the standard deviation, which controls the width of the curve.
  • $e$ is the base of the natural logarithm (approximately 2.71828).
  • $\pi$ is a mathematical constant (approximately 3.14159).

Sigma ($\sigma$) and its Impact on the Curve:

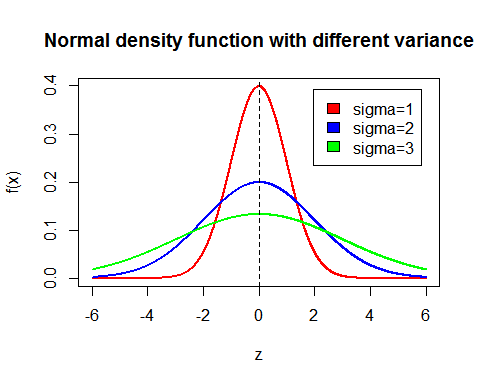
• Standard Deviation: Sigma ($\sigma$) represents the standard deviation of the Gaussian distribution. It determines how spread out the curve is.
  • Larger $\sigma$: A larger sigma value results in a wider, flatter curve. This means the blurring effect is more pronounced, and the function has a broader influence on neighboring pixels. ${\lim }_{\sigma \to \infty }G(x,y)=\frac{1}{2\pi {\sigma }^2}$
  • Smaller $\sigma$: A smaller sigma value results in a narrower, taller curve. The blurring effect is more localized, and the function primarily affects pixels closer to the center. ${\lim }_{\sigma \to 0}G(x,y)=\delta (x,y)$ where $\delta (x,y)$ is the Dirac delta function.

Gaussian Subspace

• Concept: In the context of image processing, a Gaussian subspace is not a formally defined term like in linear algebra. Instead, it’s a way to describe the set of images generated by applying Gaussian filters with a fixed sigma ($\sigma$) to an input image at different scales.

• Process:

  1. Input Image: Start with an original image, $I(x,y)$.

  2. Gaussian Filter (fixed $\sigma$): Define a Gaussian filter, $G(x,y,\sigma )$, with a specific standard deviation, $\sigma$.

  3. Scaling: Create multiple scaled versions of the input image. This is usually done by downsampling (reducing the resolution) by factors of 2. Let’s denote the scaled images as $I_s(x,y)$, where $s$ represents the scale level (e.g., $s=0$ for the original size, $s=1$ for half the size, $s=2$ for a quarter of the size, and so on).

  4. Convolution: Convolve each scaled image $I_s(x,y)$ with the same Gaussian filter $G(x,y,\sigma )$.

     $I_{s,\sigma }(x,y)=I_s(x,y)\ast G(x,y,\sigma )$

     where $\ast$ denotes the convolution operation.

• Result: The set of resulting images $\{I_{0,\sigma },I_{1,\sigma },I_{2,\sigma },\dots \}$ constitutes what is referred to as the “Gaussian subspace” for that specific $\sigma$. Each image in this set contains features that are emphasized or suppressed based on their scale and the smoothing effect of the Gaussian filter.

Benefits of Gaussian Filtering in this Context

• Smoothing and Noise Reduction: The Gaussian filter is excellent for smoothing images and reducing high-frequency noise. The weighted averaging process (inherent in the Gaussian function) effectively blurs out rapid variations in pixel intensity. $G(x,y)=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{x^2+y^2}{2{\sigma }^2}}$ Since the Gaussian function assigns higher weights to pixels closer to the center, it preserves the overall structure of the image while reducing noise.

• Scale-Space Representation: By applying the Gaussian filter at multiple scales, you create a scale-space representation of the image. This is crucial for many computer vision tasks because it allows you to analyze features at different levels of detail. $L(x,y,\sigma )=G(x,y,\sigma )\ast I(x,y)$

  where $L(x,y,\sigma )$ is the scale-space representation of the image $I(x,y)$.

• Feature Detection: Gaussian filtering is often a preprocessing step for feature detection algorithms (like edge detection or corner detection). By smoothing the image, you eliminate spurious responses caused by noise, making the feature detection more robust. ${\nabla }^{2}L(x,y,\sigma )=\frac{{\partial }^{2}L}{\partial x^2}+\frac{{\partial }^{2}L}{\partial y^2}$ The Laplacian of Gaussian (LoG) operator, which combines Gaussian smoothing with the Laplacian operator for edge detection.

• Approximation of Laplacian: The difference of Gaussians (DoG), which involves subtracting two Gaussian-filtered images with slightly different $\sigma$ values, can be used as an approximation of the Laplacian of Gaussian (LoG) operator. The LoG is used for blob detection.

  $\text{DoG}(x,y,\sigma )=G(x,y,k\sigma )\ast I(x,y)-G(x,y,\sigma )\ast I(x,y)$

  where $k$ is a constant factor.

Let me know if you would like more details on any of these aspects!

Key Considerations for Gaussian Pyramids and Image Filtering

1. Feature Distribution: When generating a Gaussian pyramid (or a scale-space representation), it is essential that the features of the original image are distributed across the different levels of the pyramid. This means that no single level should contain all the important features, nor should any significant feature be completely absent from all levels. Each scaled and filtered image in the pyramid represents a different view of the same underlying features, but at varying levels of detail.
2. No Spurious Information: A crucial requirement for any image filter, including the Gaussian filter, is that it must not introduce any artifacts or features that were not present in the original image. The filtering process should only modify existing information (e.g., by smoothing or enhancing) and should never create new, false information. This principle is especially important in applications where the accuracy of the image data is critical.